Peel the onion (optimization techniques)

The issue as expressed by original poster was that the code did not scale well using OpenMP on an 8 core E5-2650 V2 processor with 16 hardware threads. I took some time on the forum to aid the poster by giving him some pointers, but did not take sufficient time to fully optimize the code. This article will address additional optimizations that can be made beyond that laid out in the IDZ forum.
I have to say it is unclear as to the experience level of the original poster; I am going to assume he has recently graduated from an institution that may have taught parallel programming with an emphasis on scaling. In the outside world, the practicalities are: systems have limited amount of processing resources (threads), and the emphasis should be on efficiency as well as scaling. The original sample code on that forum posting provides us with the foundation of a learning tool of how to address efficiencies, in the greater sense, and scaling in the lesser sense.
In order to present code for this paper, I took the liberty to re-work the sample code, while keeping with the overall design and spirit of the original code. This means, I kept the fundamental algorithm intact as the example code was taken from an application that may have had additional functionality requiring the given algorithm. The provided code sample used an array of LOGICALs (mask) for flow control. While the sample code could have been written without the logical array(s), the sample code provided may have been an abbreviated excerpt of a larger application, and these mask arrays may have been required for reasons not obvious in the sample code. Therefore the masks were kept.
Upon inspection of the code, and the poster’s first attempt at parallelization, it was determined that the place chosen to create the parallel region (parallel DO) had too short of run. The original code can be sketched like this:
bid = 1 ! { not stated in original posting, but would appeared to be in a DO bid=1,65 }
do k=1,km-1 ! km = 60
do kk=1,2
!$OMP PARALLEL PRIVATE(I) DEFAULT(SHARED)
!$omp do
do j=1,ny_block ! ny_block = 100
do i=1,nx_block ! nx_block = 81
… {code}
enddo
enddo
!$omp end do
!$OMP END PARALLEL
enddo
enddo
For the users first attempt at parallelization he placed the parallel do on the do j= loop. While this is the “hottest” loop levels, it is not the appropriate loop level for this problem and on this platform.
The number of threads involved was 16. With 16 threads, and the inner two loops performing a combined 8100 iterations, each thread would iterate about 506 iterations. However, the parallel region would be entered 120 times (60*2). The work performed in the inner most loop, while not insignificant, was also not significant. This resulted in the cost of the parallel region being a significant portion of the application. With 16 threads, and an outer loop count of 60 iterations (120 if loops fused), a better choice may be to raise the parallel region to the do k loop.
The code was modified to execute the do k loop many times and compute the average time to execute the entire do k loop. As optimization techniques are applied, we can then use the ratios of average times of original code to revised code as a measurement of improvement. While I did not have an 8 core E5-2650 v2 processor available for testing, I do have a 6 core E5-2620 v2 processor available. The slightly reworked code presented the following results:
OriginalSerialCode
Average time 0.8267E-02
Version1_ParallelAtInnerTwoLoops
Average time 0.1746E-02, x Serial 4.74
Perfect scaling on an 6 core E5-2620 v2 processor would have been somewhere between 6x and 12x (7x if you assume an additional 15% for HT). A scaling of 4.74x is significantly less than an expected 7x.
In the following sections of this paper will walk you through four additional techniques of optimization.
OriginalSerialCode
Average time 0.8395E-02
ParallelAtInnerTwoLoops
Average time 0.1699E-02, x Serial 4.94
ParallelAtkmLoop
Average time 0.6905E-03, x Serial 12.16, x Prior 2.46
ParallelAtkmLoopDynamic
Average time 0.5509E-03, x Serial 15.24, x Prior 1.25
ParallelNestedRank1
Average time 0.3630E-03, x Serial 23.13, x Prior 1.52
Note, the ParallelAtInnerTwoLoops report in the second run illustrates a different multiplier factor than the first run. The principal cause for this is fortuitous code placement or lack thereof. The code did not change between runs. The only difference was the addition of the extra code and the insertion of the call statements to run those subroutines. It is important to bear in mind that code placement of tight loops can significantly affect the performance of those loops. Even adding or removing a single statement can significantly affect some code run times.
To facilitate ease of reading of the code changes, the body of the inner 3 loops was encapsulated into a subroutine. This makes the code easier to study as well as easier to diagnose with program profiler (VTune). Example from the ParallelAtkmLoop subroutine:
bid = 1
!$OMP PARALLEL DEFAULT(SHARED)
!$omp do
do k=1,km-1 ! km = 60
call ParallelAtkmLoop_sub(bid, k)
end do
!$omp end do
!$OMP END PARALLEL
endtime = omp_get_wtime()
…
subroutine ParallelAtkmLoop_sub(bid, k)
…
do kk=1,2
do j=1,ny_block ! ny_block = 100
do i=1,nx_block ! nx_block = 81
…
enddo
enddo
enddo
end subroutine ParallelAtkmLoop_sub
The first optimization I performed was to make two changes:
1) Move the parallelization up two loop levels to the do k loop level. Thus reducing the number of entries into the parallel region by a factor of 120. And,
2) The application used an array of LOGICAL’s as a mask for code selection. I reworked the code used to generate the values to reduce unnecessary manipulation of the mask array.
These two changes resulted in an improvement of 2.46x over the initial parallelization attempt. While this improvement is great, is this as good as you can get?
In looking at the code of the inner most loop we find:
… {construct masks}
if ( LMASK1(i,j) ) then
… {code}
endif
if ( LMASK2(i,j) ) then
… {code}
endif
if( LMASK3(i,j) ) then
… {code}
endif
Meaning the filter masks results in the work load per iteration being unequal. Under this circumstance, it is often better to use dynamic scheduling. This next optimization is performed with ParallelAtkmLoopDynamic. This is the same code as ParallelAtkmLoop but with schedule(dynamic) added to the !$omp do.
This simple change added an additional 1.25x. Note, dynamic scheduling is not your only scheduling option. There are others that might be worth exploring, and note that the type of scheduling often includes a modifier clause (chunk size).
The next level of optimization, which provides an additional 1.52x performance boost in performance, is what one would consider aggressive optimization. The extra 52% does require significant programming effort (but not unmanageable). The opportunity for this optimization comes from an observation that can be made by looking at the Assembly code that you can view using VTune.
I would like to stress that you do not have to understand the assembly code when you look at it. In general you can assume:
more assembly code == slower performance
What you can do is to make an inference as to the complexity (volume) of assembly code has to potential missed optimization opportunities by the compiler. And, when missed opportunities are detected, how you can use a simple technique, to aid the complier with code optimization.
When looking at the body of main work we find:
subroutine ParallelAtkmLoopDynamic_sub(bid, k)
use omp_lib
use mod_globals
implicit none
!———————————————————————–
!
! dummy variables
!
!———————————————————————–
integer :: bid,k
!———————————————————————–
!
! local variables
!
!———————————————————————–
real , dimension(nx_block,ny_block,2) :: &
WORK1, WORK2, WORK3, WORK4 ! work arrays
real , dimension(nx_block,ny_block) :: &
WORK2_NEXT, WORK4_NEXT ! WORK2 or WORK4 at next level
logical , dimension(nx_block,ny_block) :: &
LMASK1, LMASK2, LMASK3 ! flags
integer :: kk, j, i ! loop indices
!———————————————————————-
!
! code
!
!———————————————————————–
do kk=1,2
do j=1,ny_block
do i=1,nx_block
if(TLT%K_LEVEL(i,j,bid) == k) then
if(TLT%K_LEVEL(i,j,bid) < KMT(i,j,bid)) then
LMASK1(i,j) = TLT%ZTW(i,j,bid) == 1
LMASK2(i,j) = TLT%ZTW(i,j,bid) == 2
if(LMASK2(i,j)) then
LMASK3(i,j) = TLT%K_LEVEL(i,j,bid) + 1 < KMT(i,j,bid)
else
LMASK3(i,j) = .false.
endif
else
LMASK1(i,j) = .false.
LMASK2(i,j) = .false.
LMASK3(i,j) = .false.
endif
else
LMASK1(i,j) = .false.
LMASK2(i,j) = .false.
LMASK3(i,j) = .false.
endif
if ( LMASK1(i,j) ) then
WORK1(i,j,kk) = KAPPA_THIC(i,j,kbt,k,bid) &
* SLX(i,j,kk,kbt,k,bid) * dz(k)
WORK2(i,j,kk) = c2 * dzwr(k) * ( WORK1(i,j,kk) &
– KAPPA_THIC(i,j,ktp,k+1,bid) * SLX(i,j,kk,ktp,k+1,bid) &
* dz(k+1) )
WORK2_NEXT(i,j) = c2 * ( &
KAPPA_THIC(i,j,ktp,k+1,bid) * SLX(i,j,kk,ktp,k+1,bid) – &
KAPPA_THIC(i,j,kbt,k+1,bid) * SLX(i,j,kk,kbt,k+1,bid) )
WORK3(i,j,kk) = KAPPA_THIC(i,j,kbt,k,bid) &
* SLY(i,j,kk,kbt,k,bid) * dz(k)
WORK4(i,j,kk) = c2 * dzwr(k) * ( WORK3(i,j,kk) &
– KAPPA_THIC(i,j,ktp,k+1,bid) * SLY(i,j,kk,ktp,k+1,bid) &
* dz(k+1) )
WORK4_NEXT(i,j) = c2 * ( &
KAPPA_THIC(i,j,ktp,k+1,bid) * SLY(i,j,kk,ktp,k+1,bid) – &
KAPPA_THIC(i,j,kbt,k+1,bid) * SLY(i,j,kk,kbt,k+1,bid) )
if( abs( WORK2_NEXT(i,j) ) < abs( WORK2(i,j,kk) ) ) then
WORK2(i,j,kk) = WORK2_NEXT(i,j)
endif
if ( abs( WORK4_NEXT(i,j) ) < abs( WORK4(i,j,kk ) ) ) then
WORK4(i,j,kk) = WORK4_NEXT(i,j)
endif
endif
if ( LMASK2(i,j) ) then
WORK1(i,j,kk) = KAPPA_THIC(i,j,ktp,k+1,bid) &
* SLX(i,j,kk,ktp,k+1,bid)
WORK2(i,j,kk) = c2 * ( WORK1(i,j,kk) &
– ( KAPPA_THIC(i,j,kbt,k+1,bid) &
* SLX(i,j,kk,kbt,k+1,bid) ) )
WORK1(i,j,kk) = WORK1(i,j,kk) * dz(k+1
WORK3(i,j,kk) = KAPPA_THIC(i,j,ktp,k+1,bid) &
* SLY(i,j,kk,ktp,k+1,bid
WORK4(i,j,kk) = c2 * ( WORK3(i,j,kk) &
– ( KAPPA_THIC(i,j,kbt,k+1,bid) &
* SLY(i,j,kk,kbt,k+1,bid) ) )
WORK3(i,j,kk) = WORK3(i,j,kk) * dz(k+1)
endif
if( LMASK3(i,j) ) then
if (k.lt.km-1) then ! added to avoid out of bounds access
WORK2_NEXT(i,j) = c2 * dzwr(k+1) * ( &
KAPPA_THIC(i,j,kbt,k+1,bid) * SLX(i,j,kk,kbt,k+1,bid) * dz(k+1) – &
KAPPA_THIC(i,j,ktp,k+2,bid) * SLX(i,j,kk,ktp,k+2,bid) * dz(k+2))
WORK4_NEXT(i,j) = c2 * dzwr(k+1) * ( &
KAPPA_THIC(i,j,kbt,k+1,bid) * SLY(i,j,kk,kbt,k+1,bid) * dz(k+1) – &
KAPPA_THIC(i,j,ktp,k+2,bid) * SLY(i,j,kk,ktp,k+2,bid) * dz(k+2))
end if
if( abs( WORK2_NEXT(i,j) ) < abs( WORK2(i,j,kk) ) ) &
WORK2(i,j,kk) = WORK2_NEXT(i,j)
if( abs(WORK4_NEXT(i,j)) < abs(WORK4(i,j,kk)) ) &
WORK4(i,j,kk) = WORK4_NEXT(i,j)
endif
enddo
enddo
enddo
end subroutine Version2_ParallelAtkmLoop_sub
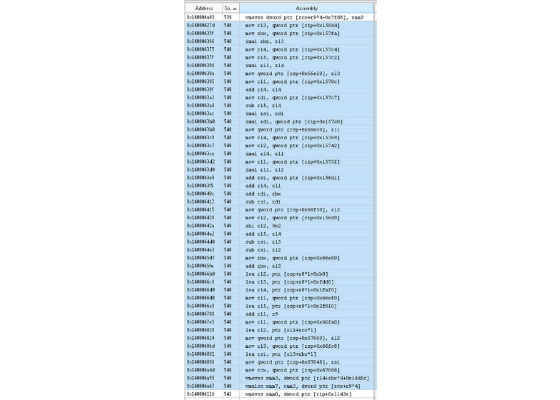
Making an Intel Amplifier run (VTune), and looking at line 540 as an example:
We have part of a statement that performs the product of two numbers. For this partial statement you would expect:
Load value at some index of SLX
Multiply by value at some index of dz
Clicking on the Assembly button in amplifier:
Then, sorting by source line number:
And locating source line 540, we find:
We find a total of 46 assembler instructions use to multiply two numbers.
Now comes the inference part.
The two numbers are cells of two arrays. The array SLX has six subscripts the other has one subscript. You can also observe that the last two assembly instructions are vmovss from memory and vmulss from memory. We were expecting fully optimized code to produce something similar to our expectations. The code above shows 44 out of 46 assembly instructions are associated with computing the array indexes to these two variables. Granted, we might expect a few instructions to obtain the indexes into the arrays, but not 44 instructions. Can we do something to reduce this complexity?
In looking at the source code (most recent above) you will note that the last four subscripts of SLX, and the one subscript of dz are loop invariant for the inner most two loops. In the case of SLX, the left most two indices, the inner most two loop control variables, represents a contiguous array section. The compiler optimization failed to recognize the unchanging (right most) array indices as candidates for loop invariant code that can be lifted out of a loop. Additionally, the compiler also failed to identify the left two most indexes as a candidate for collapse into a single index.
This is a good example of what future compiler optimization efforts could address under these circumstances. In this case, the next optimization, which performs a lifting of loop invariant subscripting, illustrates a 1.52x performance boost.
Now that we know that a goodly portion of the “do work” code involves contiguous array sections with several subscripts, can we somehow reduce the number of subscripts without rewriting the application?
The answer to this is yes, if we encapsulate smaller array slices represented by fewer array subscripts. How do we do this for this example code?
The choice made was for two nest levels:
at the outer most bid level (the module data indicates the actual code uses 65 bid values)
at the next to outer most level, the do k loop level. In addition to this, we consolidate the first two indexes into one.
The outermost level passes bid level array sections:
bid = 1 ! in real application bid may iterate
! peel off the bid
call ParallelNestedRank1_bid( &
TLT%K_LEVEL(:,:,bid), &
KMT(:,:,bid), &
TLT%ZTW(:,:,bid), &
KAPPA_THIC(:,:,:,:,bid), &
SLX(:,:,:,:,:,bid), &
SLY(:,:,:,:,:,bid))
…
subroutine ParallelNestedRank1_bid(K_LEVEL_bid, KMT_bid, ZTW_bid, KAPPA_THIC_bid, SLX_bid, SLY_bid)
use omp_lib
use mod_globals
implicit none
integer, dimension(nx_block , ny_block) :: K_LEVEL_bid, KMT_bid, ZTW_bid
real, dimension(nx_block,ny_block,2,km) :: KAPPA_THIC_bid
real, dimension(nx_block,ny_block,2,2,km) :: SLX_bid, SLY_bid
…
Note, for non-pointer (allocatable or fixed dimensioned) arrays, the arrays are contiguous. This provides you with the opportunity to peel off the right most indexes to pass on a contiguous array section, and do so with merely computing the offset to the subsection of the larger array. Whereas peeling indexes other than rightmost would require creating a temporary array, and should be avoided. Though there may be some cases where it might be beneficial to do so.
And the second nested level peeled off an additional array index of the do k loop, as well as compressed the first two indexes into one:
!$OMP PARALLEL DEFAULT(SHARED)
!$omp do
do k=1,km-1
call ParallelNestedRank1_bid_k( &
K_LEVEL_bid, KMT_bid, ZTW_bid, &
KAPPA_THIC_bid(:,:,:,k), &
KAPPA_THIC_bid(:,:,:,k+1), KAPPA_THIC_bid(:,:,:,k+2),&
SLX_bid(:,:,:,:,k), SLY_bid(:,:,:,:,k), &
SLX_bid(:,:,:,:,k+1), SLY_bid(:,:,:,:,k+1), &
SLX_bid(:,:,:,:,k+2), SLY_bid(:,:,:,:,k+2), &
dz(k),dz(k+1),dz(k+2),dzwr(k),dzwr(k+1))
end do
!$omp end do
!$OMP END PARALLEL
end subroutine ParallelNestedRank1_bid
subroutine ParallelNestedRank11_bid_k( &
k, K_LEVEL_bid, KMT_bid, ZTW_bid, &
KAPPA_THIC_bid_k, KAPPA_THIC_bid_kp1, KAPPA_THIC_bid_kp2, &
SLX_bid_k, SLY_bid_k, &
SLX_bid_kp1, SLY_bid_kp1, &
SLX_bid_kp2, SLY_bid_kp2, &
dz_k,dz_kp1,dz_kp2,dzwr_k,dzwr_kp1)
use mod_globals
implicit none
!———————————————————————–
!
! dummy variables
!
!———————————————————————–
integer :: k
integer, dimension(nx_block*ny_block) :: K_LEVEL_bid, KMT_bid, ZTW_bid
real, dimension(nx_block*ny_block,2) :: KAPPA_THIC_bid_k, KAPPA_THIC_bid_kp1
real, dimension(nx_block*ny_block,2) :: KAPPA_THIC_bid_kp2
real, dimension(nx_block*ny_block,2,2) :: SLX_bid_k, SLY_bid_k
real, dimension(nx_block*ny_block,2,2) :: SLX_bid_kp1, SLY_bid_kp1
real, dimension(nx_block*ny_block,2,2) :: SLX_bid_kp2, SLY_bid_kp2
real :: dz_k,dz_kp1,dz_kp2,dzwr_k,dzwr_kp1
… ! next note index (i,j) compression to (ij)
do kk=1,2
do ij=1,ny_block*nx_block
if ( LMASK1(ij) ) then
Note that at the point of the call, a contiguous array section (reference) is passed. The dummy arguments of the called routine specify a same sized contiguous chunk of memory with a different number of indexes. As long as you are careful in Fortran, you can do this.
The coding effort was mostly a copy and paste, then a find and replace operation. Other than this, there was no code flow changes. A meticulous junior programmer could have done this with proper instructions.
While future versions of compiler optimization may make this unnecessary, a little bit of “unnecessary” programming effort now can, at times, yield substantial performance gains (52% in this case).
The equivalent source code statement is now:
And the assembly code is now:
We are now down from 46 instructions to 6 instructions a 7.66x reduction. This illustrates that by reducing the number of array subscripts, that the complier optimization can reduce the instruction count.
Introducing a 2-Level nest with peel yielded a 1.52x performance boost. As to if a 52% boost in performance is worth the additional effort, this is a subjective measure for you to decide. I anticipate that future compiler optimizations will perform loop invariant array subscript lifting as performed manually above. But until then you can use the index peel and compress technique.
For more such intel Modern Code and tools from Intel, please visit the Intel® Modern Code
Source:https://software.intel.com/en-us/articles/peel-the-onion-optimization-techniques